239. Sliding Window Maximum
- 在一個整數陣列中,找到每個滑動�視窗中的最大值。函式接收兩個參數:一個是整數陣列
nums,另一個是滑動視窗的大小k。 - 初始化一個 deque
q,用來儲存滑動視窗中有潛力成為最大值的元素的 index。
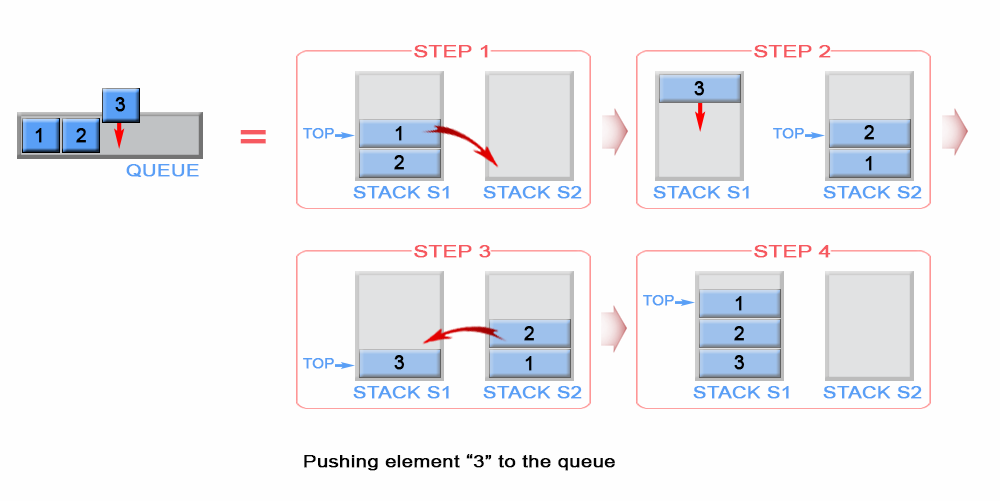
deque
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k)
{
int n = nums.size();
vector<int> res;
deque<int> q;
for (int i = 0; i < n; ++i)
{
// 因為滑動視窗會向前移動
// 當 q.front() 的元素離開視窗的時候
// 1 [3 -1 -3]
// ^ ^
// <- k -> i
if (!q.empty() && q.front() + k == i)
{
q.pop_front();
}
// 當發現 deque 尾端的元素比目前的 nums[i] 小的時候
// pop 掉,因為不可能成為最大值
// 所以 deque 裡面會存有潛力成為最大值數字的 index
while (!q.empty() && nums[q.back()] < nums[i])
{
q.pop_back();
}
// 將 index push 到 queue
q.push_back(i);
// 當發現 i + 1 >= k 的時候
// 代表滑動視窗的大小 k 已經形成
// 則將最大值 nums[q.front()] 推到 res
if (i + 1 >= k)
{
res.push_back(nums[q.front()]);
}
}
return res;
}
};
- T: $O(n)$
- S: $O(k)$
priority queue
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k)
{
vector<int> res;
// 預設由大排到小
priority_queue<pair<int, int>> q;
for (int i = 0; i < nums.size(); ++i)
{
while (!q.empty() && q.top().second <= i - k)
{
q.pop();
}
// {存數字, 存 index}
q.push({nums[i], i});
// 如果滑動視窗形成
// 將最大值 push 到 res
if (i >= k - 1)
{
res.push_back(q.top().first);
}
}
return res;
}
};
- T: $O(n)$
- S: $O(k)$